This is an old revision of this page, as edited by Dedhert.Jr (talk | contribs) at 03:57, 20 March 2024 (→Properties: point groups). The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.
Revision as of 03:57, 20 March 2024 by Dedhert.Jr (talk | contribs) (→Properties: point groups)(diff) ← Previous revision | Latest revision (diff) | Newer revision → (diff) 37th Johnson solid| This article or section is in a state of significant expansion or restructuring. You are welcome to assist in its construction by editing it as well. If this article or section has not been edited in several days, please remove this template. If you are the editor who added this template and you are actively editing, please be sure to replace this template with {{in use}} during the active editing session. Click on the link for template parameters to use.
This article was last edited by Dedhert.Jr (talk | contribs) 10 months ago. (Update timer) |
| Elongated square gyrobicupola | |
|---|---|
 | |
| Type | Johnson J36 – J37 – J38 |
| Faces | 8 triangles 18 squares |
| Edges | 48 |
| Vertices | 24 |
| Vertex configuration | 8+16(3.4) |
| Symmetry group | D4d |
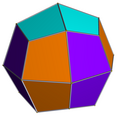
| Dual polyhedron | Pseudo-deltoidal icositetrahedron |
| Properties | convex, singular vertex figure, canonical |
| Net | |
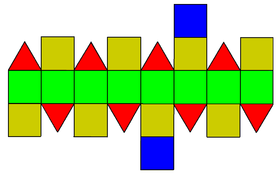 | |
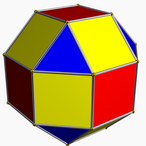
In geometry, the elongated square gyrobicupola or pseudo-rhombicuboctahedron is one of the Johnson solids (J37). It is not usually considered to be an Archimedean solid, even though its faces consist of regular polygons that meet in the same pattern at each of its vertices, because unlike the 13 Archimedean solids, it lacks a set of global symmetries that map every vertex to every other vertex (though Grünbaum has suggested it should be added to the traditional list of Archimedean solids as a 14th example). It strongly resembles, but should not be mistaken for, the rhombicuboctahedron, which is an Archimedean solid. It is also a canonical polyhedron.
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.
Construction
The elongated square gyrobicupola can be constructed similarly to the rhombicuboctahedron, by attaching two regular square cupolas onto the bases of octagonal prism, a process known as elongation. The difference between these two polyhedrons is that one of two square cupolas of the elongated square gyrobicupola is twisted by 45 degrees, a process known as gyro, making the triangular faces staggered vertically. The resulting polyhedron has 8 equilateral triangles and 18 squares. A convex polyhedron in which all of the faces are regular polygons is the Johnson solid, and the elongated square gyrobicupola is among them, enumerated as the 37th Johnson solid .

 Process of the construction of the elongated square gyrobicupola
Process of the construction of the elongated square gyrobicupola
The elongated square gyrobicupola may have been discovered by Johannes Kepler in his enumeration of the Archimedean solids, but its first clear appearance in print appears to be the work of Duncan Sommerville in 1905. It was independently rediscovered by J. C. P. Miller in 1930 by mistake while attempting to construct a model of the rhombicuboctahedron, which is known as psuedo-rhombicuboctahedron or sometimes Miller's solid. This solid was discovered again by V. G. Ashkinuse in 1957.
Properties
An elongated square gyrobicupola with edge length has a surface area: by adding the area of 8 equilateral triangles and 10 squares. Its volume can be calculated by slicing it into two square cupolas and one octagonal prism:

The elongated square gyrobicupola possesses three-dimensional symmetry group of order 16. It is locally vertex-regular – the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, the manner in which it is "twisted" gives it a distinct "equator" and two distinct "poles", which in turn divides its vertices into 8 "polar" vertices (4 per pole) and 16 "equatorial" vertices. It is therefore not vertex-transitive, and consequently not usually considered to be one of the Archimedean solids.
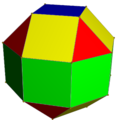
With faces colored by its D4d symmetry, it can look like this:
| The pseudo-deltoidal icositetrahedron (right) is the dual polyhedron. | |
|
|
There are 8 (green) squares around its equator, 4 (red) triangles and 4 (yellow) squares above and below, and one (blue) square on each pole.
Related polyhedra and honeycombs
The elongated square gyrobicupola can form a space-filling honeycomb with the regular tetrahedron, cube, and cuboctahedron. It can also form another honeycomb with the tetrahedron, square pyramid and various combinations of cubes, elongated square pyramids, and elongated square bipyramids.

The pseudo great rhombicuboctahedron is a nonconvex analog of the pseudo-rhombicuboctahedron, constructed in a similar way from the nonconvex great rhombicuboctahedron.
In chemistry
The polyvanadate ion has a pseudo-rhombicuboctahedral structure, where each square face acts as the base of a VO5 pyramid.
References
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ^ Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
- ^ Cromwell, Peter R. (1997), Polyhedra, Cambridge University Press, p. 91, ISBN 978-0-521-55432-9.
- Francis, Darryl (August 2013), "Johnson solids & their acronyms", Word Ways, 46 (3): 177.
- Sommerville, D. M. Y. (1905), "Semi-regular networks of the plane in absolute geometry", Transactions of the Royal Society of Edinburgh, 41: 725–747, doi:10.1017/s0080456800035560. As cited by Grünbaum (2009).
- Ball, Rouse (1939), Coxeter, H. S. M. (ed.), Mathematical recreations and essays (11 ed.), p. 137.
- Grünbaum, Branko (2009), "An enduring error" (PDF), Elemente der Mathematik, 64 (3): 89–101, doi:10.4171/EM/120, MR 2520469 Reprinted in Pitici, Mircea, ed. (2011). The Best Writing on Mathematics 2010. Princeton University Press. pp. 18–31..
- Lando, Sergei K.; Zvonkin, Alexander K. (2004), Graphs on Surfaces and Their Applications, Springer, p. 114, doi:10.1007/978-3-540-38361-1, ISBN 978-3-540-38361-1.
- "J37 honeycombs", Gallery of Wooden Polyhedra, retrieved 2016-03-21
- Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. p. 986. ISBN 978-0-08-037941-8.
Further reading
- Anthony Pugh (1976), Polyhedra: A visual approach, California: University of California Press Berkeley, ISBN 0-520-03056-7 Chapter 2: Archimedean polyhedra, prisma and antiprisms, p. 25 Pseudo-rhombicuboctahedron
External links
- Weisstein, Eric W., "Elongated square gyrobicupola" ("Johnson solid") at MathWorld.
- George Hart: pseudo-rhombicuboctahedra
 .
.
 has a surface area:
has a surface area:
 by adding the area of 8 equilateral triangles and 10 squares. Its volume can be calculated by slicing it into two square cupolas and one octagonal prism:
by adding the area of 8 equilateral triangles and 10 squares. Its volume can be calculated by slicing it into two square cupolas and one octagonal prism:

 of order 16. It is locally vertex-regular – the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, the manner in which it is "twisted" gives it a distinct "equator" and two distinct "poles", which in turn divides its vertices into 8 "polar" vertices (4 per pole) and 16 "equatorial" vertices. It is therefore not
of order 16. It is locally vertex-regular – the arrangement of the four faces incident on any vertex is the same for all vertices; this is unique among the Johnson solids. However, the manner in which it is "twisted" gives it a distinct "equator" and two distinct "poles", which in turn divides its vertices into 8 "polar" vertices (4 per pole) and 16 "equatorial" vertices. It is therefore not